Derivatives play a main function in optimization and artificial intelligence. By in your area estimating a training loss, derivatives assist an optimizer towards lower worths of the loss. Automatic distinction structures such as TensorFlow, PyTorch, and JAX are a vital part of contemporary artificial intelligence, making it possible to utilize gradient-based optimizers to train really complicated designs.
However are derivatives all we require? On their own, derivatives just inform us how a function acts on an infinitesimal scale. To utilize derivatives efficiently, we typically require to understand more than that. For instance, to select a discovering rate for gradient descent, we require to understand something about how the loss function acts over a little however limited window. A finite-scale analogue of automated distinction, if it existed, might assist us make such options better and consequently accelerate training.
In our brand-new paper “ Instantly Bounding The Taylor Rest Series: Tighter Bounds and New Applications“, we provide an algorithm called AutoBound that calculates polynomial upper and lower bounds on an offered function, which stand over a user-specified period We then start to check out AutoBound’s applications. Significantly, we provide a meta-optimizer called SafeRate that utilizes the upper bounds calculated by AutoBound to obtain knowing rates that are ensured to monotonically lower an offered loss function, without the requirement for lengthy hyperparameter tuning. We are likewise making AutoBound offered as an open-source library
The AutoBound algorithm
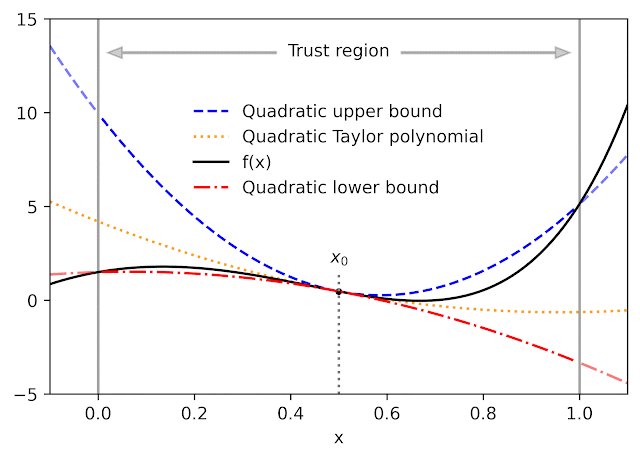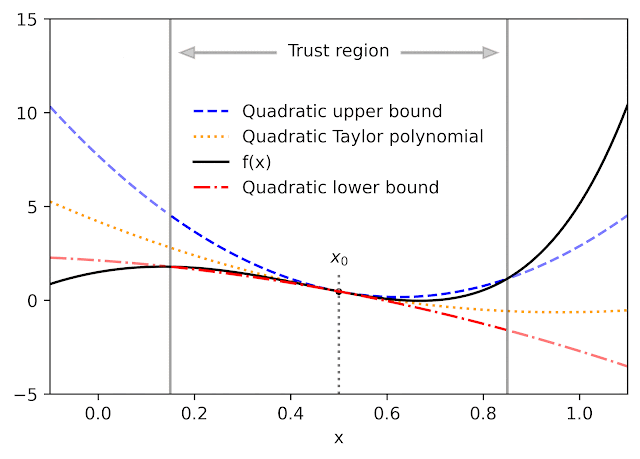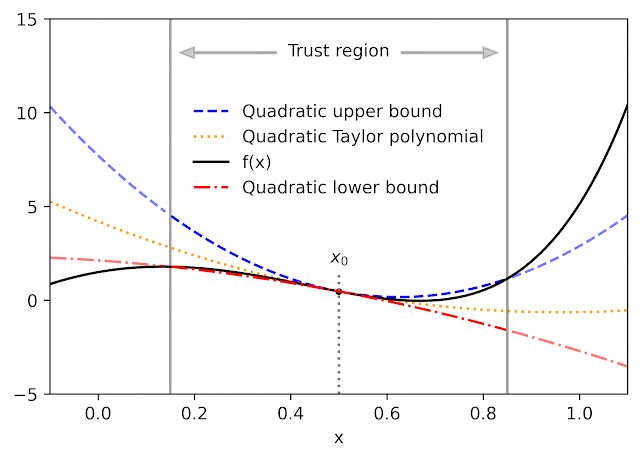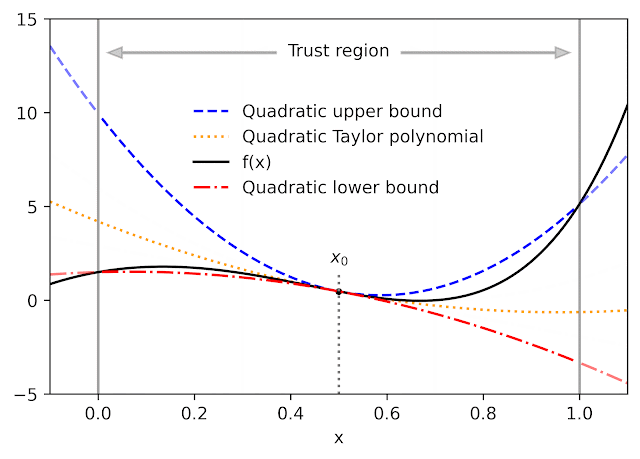
Provided a function f and a recommendation point x 0, AutoBound calculates polynomial upper and lower bounds on f that hold over a user-specified period called a trust area Like Taylor polynomials, the bounding polynomials amount to f at x 0 The bounds end up being tighter as the trust area diminishes, and approach the matching Taylor polynomial as the trust area width approaches absolutely no.
 |
| Automatically-derived quadratic upper and lower bounds on a one-dimensional function f, focused at x 0= 0.5. The upper and lower bounds stand over a user-specified trust area, and end up being tighter as the trust area diminishes. |
Like automated distinction, AutoBound can be used to any function that can be executed utilizing basic mathematical operations. In reality, AutoBound is a generalization of Taylor mode automated distinction, and is comparable to it in the diplomatic immunity where the trust area has a width of absolutely no.
To obtain the AutoBound algorithm, there were 2 primary obstacles we needed to address:.
- We needed to obtain polynomial upper and lower bounds for numerous primary functions, offered an approximate referral point and approximate trust area.
- We needed to develop an analogue of the chain guideline for integrating these bounds.
Bounds for primary functions
For a range of commonly-used functions, we obtain optimum polynomial upper and lower bounds in closed kind. In this context, “optimum” implies the bounds are as tight as possible, amongst all polynomials where just the optimum- degree coefficient varies from the Taylor series. Our theory uses to primary functions, such as exp and log, and typical neural network activation functions, such as ReLU and Swish It builds on and generalizes earlier work that used just to quadratic bounds, and just for an unbounded trust area.
 |
| Optimum quadratic upper and lower bounds on the rapid function, focused at x 0= 0.5 and legitimate over the period [0, 2]. |
A brand-new chain guideline
To calculate upper and lower bounds for approximate functions, we obtained a generalization of the chain guideline that runs on polynomial bounds. To highlight the concept, expect we have a function that can be composed as.
and expect we currently have polynomial upper and lower bounds on g and h How do we calculate bounds on f?
The crucial ends up being representing the upper and lower bounds for an offered function as a single polynomial whose highest-degree coefficient is an period instead of a scalar. We can then plug the bound for h into the bound for g, and transform the outcome back to a polynomial of the exact same kind utilizing interval math Under ideal presumptions about the trust area over which the bound on g holds, it can be revealed that this treatment yields the preferred bound on f
 |
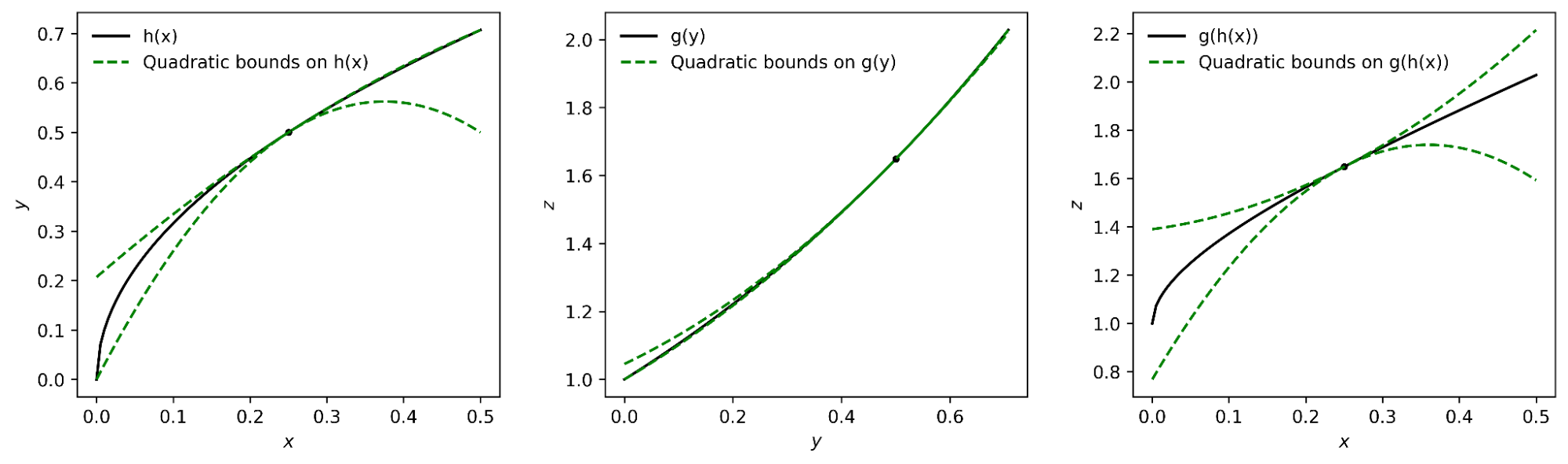| The interval polynomial chain guideline used to the functions h( x) = sqrt( x) and g( y) = exp( y), with x 0= 0.25 and trust area [0, 0.5]. |
Our chain guideline uses to one-dimensional functions, however likewise to multivariate functions, such as matrix reproductions and convolutions.
Propagating bounds
Utilizing our brand-new chain guideline, AutoBound propagates interval polynomial bounds through a calculation chart from the inputs to the outputs, comparable to forward-mode automated distinction
 |
| Forward proliferation of interval polynomial bounds for the function f( x) = exp( sqrt( x)). We initially calculate (unimportant) bounds on x, then utilize the chain guideline to calculate bounds on sqrt( x) and exp( sqrt( x)). |
To calculate bounds on a function f( x), AutoBound needs memory proportional to the measurement of x For this factor, useful applications use AutoBound to functions with a little number of inputs. Nevertheless, as we will see, this does not avoid us from utilizing AutoBound for neural network optimization.
Instantly obtaining optimizers, and other applications
What can we finish with AutoBound that we could not finish with automated distinction alone?
To name a few things, AutoBound can be utilized to instantly obtain problem-specific, hyperparameter-free optimizers that assemble from any beginning point. These optimizers iteratively lower a loss by very first utilizing AutoBound to calculate an upper bound on the loss that is tight at the present point, and after that reducing the upper bound to acquire the next point.
 |
| Lessening a one-dimensional logistic regression loss utilizing quadratic upper bounds obtained instantly by AutoBound. |
Optimizers that utilize upper bounds in this method are called majorization-minimization (MM) optimizers. Applied to one-dimensional logistic regression, AutoBound rederives an MM optimizer very first released in 2009 Applied to more complicated issues, AutoBound obtains unique MM optimizers that would be hard to obtain by hand.
We can utilize a comparable concept to take an existing optimizer such as Adam and transform it to a hyperparameter-free optimizer that is ensured to monotonically lower the loss (in the full-batch setting). The resulting optimizer utilizes the exact same upgrade instructions as the initial optimizer, however customizes the knowing rate by reducing a one-dimensional quadratic upper bound obtained by AutoBound. We describe the resulting meta-optimizer as SafeRate.
 |
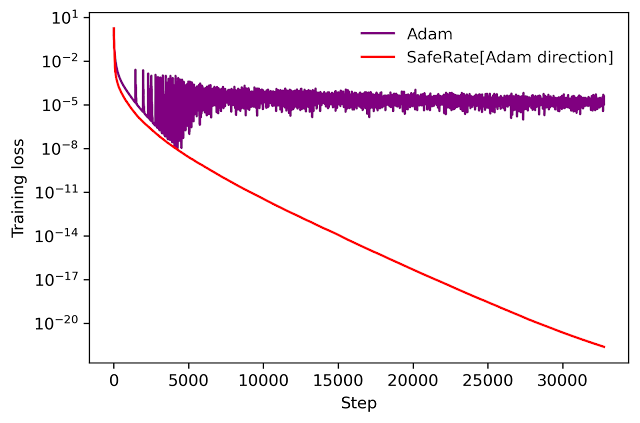| Efficiency of SafeRate when utilized to train a single-hidden-layer neural network on a subset of the MNIST dataset, in the full-batch setting. |
Utilizing SafeRate, we can produce more robust versions of existing optimizers, at the expense of a single extra forward pass that increases the wall time for each action by a little element (about 2x in the example above).
In addition to the applications simply talked about, AutoBound can be utilized for validated mathematical combination and to instantly show sharper variations of Jensen’s inequality, a basic mathematical inequality utilized often in stats and other fields.
Enhancement over classical bounds
Bounding the Taylor rest term instantly is not an originality. A classical strategy produces degree k polynomial bounds on a function f that stand over a trust area [a, b] by very first calculating an expression for the k th derivative of f (utilizing automated distinction), then assessing this expression over [a,b] utilizing interval math.
While stylish, this technique has some fundamental constraints that can result in really loose bounds, as highlighted by the dotted blue lines in the figure listed below.
 |
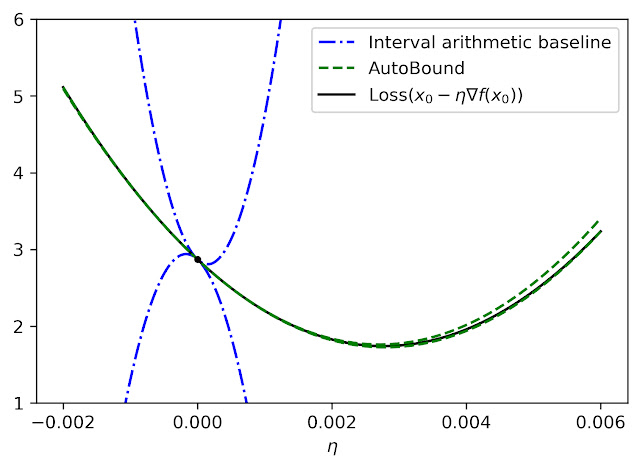| Quadratic upper and lower bounds on the loss of a multi-layer perceptron with 2 concealed layers, as a function of the preliminary knowing rate. The bounds obtained by AutoBound are much tighter than those acquired utilizing interval math assessment of the 2nd derivative. |
Looking forward
Taylor polynomials have actually remained in usage for over 3 a century, and are universal in mathematical optimization and clinical computing. Nonetheless, Taylor polynomials have substantial constraints, which can restrict the abilities of algorithms constructed on top of them. Our work becomes part of a growing literature that acknowledges these constraints and looks for to establish a brand-new structure upon which more robust algorithms can be constructed.
Our experiments up until now have actually just scratched the surface area of what is possible utilizing AutoBound, and our company believe it has lots of applications we have actually not found. To motivate the research study neighborhood to check out such possibilities, we have actually made AutoBound offered as an open-source library constructed on top of JAX To start, visit our GitHub repo
Recognitions
This post is based upon joint deal with Josh Dillon. We thank Alex Alemi and Sergey Ioffe for important feedback on an earlier draft of the post.